1. 1D Winograd 实现 (50pts)

背景知识

1. Winograd算法是一种用于加速卷积运算的高效算法，尤其在深度学习的卷积神经网络（CNN）中广泛应用。它通过减少乘法次数来优化计算，特别适合小尺寸卷积核。

2. Winograd算法的核心思想是将卷积转化为多项式乘法，利用数论中的一些变换，将输入和滤波器映射到另一个空间进行更高效的计算。

• 例如对于一维卷积：

  对于输入$d = [d_0, d_1, d_2, d_3]$和滤权重$g = [g_0, g_1, g_2]$，输出为2个元素。

  • 原始计算方法：需6次乘法与4次加法。
  • Winograd算法：通过变换将乘法次数降至4次（加法次数增加到8次），步骤如下：
    1. 将计算表示为：

    $$F(2,3) = \begin{bmatrix} d_0 & d_1 & d_2\\ d_1 & d_2 & d_3\end{bmatrix}\begin{bmatrix} g_0 \\ g_1 \\g_2\end{bmatrix}= \begin{bmatrix} m_1 + m_2 + m_3 \\ m_2 - m_3 - m_4\end{bmatrix}$$

    其中：

    $$m_1=(d_0-d_2)g_0\\ m_2=(d_1+d_2)\frac{g_0+g_1+g_2}{2}\\ m_3=(d_2-d_1)\frac{g_0-g_1+g_2}{2}\\ m_4=(d_1-d_3)g_2$$

    2. 将上面的计算过程写成矩阵的形式如下：$Y = A^T[(Gg)\odot (B^Td)]$，其中：
       • $\odot$ 表示 Hadamard product，即对应位置相乘操作；
       • $g$ 表示卷积核；$d$ 表示输入特征图（输入信号）；
       • $G$ 表示卷积核变换矩阵；
       • $B^T$ 表示输入变换矩阵；
       • $A^T$表示输出变换矩阵；

       有：

       $$B^T=\begin{bmatrix} 1 & 0 & -1 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & -1 & 1 & 0 \\ 0 & 1 & 0 & -1\end{bmatrix} \qquad G=\begin{bmatrix}1 & 0 & 0 \\\frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} \\0 & 0 & 1 \\\end{bmatrix} \\ A^T = \begin{bmatrix} 1 & 1 & 1 & 0 \\ 0 & 1 & -1 & -1 \\\end{bmatrix} \\ g = \begin{bmatrix}g_0 & g_1 & g_2\end{bmatrix}^T \qquad \qquad d = \begin{bmatrix}d_0 & d_1 & d_2 & d_3\end{bmatrix}^T$$

• 二维扩展：

  通过嵌套一维变换实现，如$F(2\times2, 3\times3)$，输入块为$4\times4$，输出为$2\times2$，乘法次数从36次降至16次。

任务介绍

本次Lab中，你需要实现一个卷积核大小固定的 1D winograd 卷积计算单元。计算单元的部分代码已经提供，你需要填补空缺的代码。

TOP module 位于 winograd_1d.v 中，虽然1D winograd可以完全通过组合逻辑完成计算，但是这会导致较大的延迟，阻碍系统时钟加快，因此，在此模块中我们将计算分为若干个阶段：

• 阶段1: 完成卷积核变换及输入变换；

• 阶段2: 完成Hadamard product与输出变换；

• 阶段3: 锁存计算结果并输出， vld 置1.

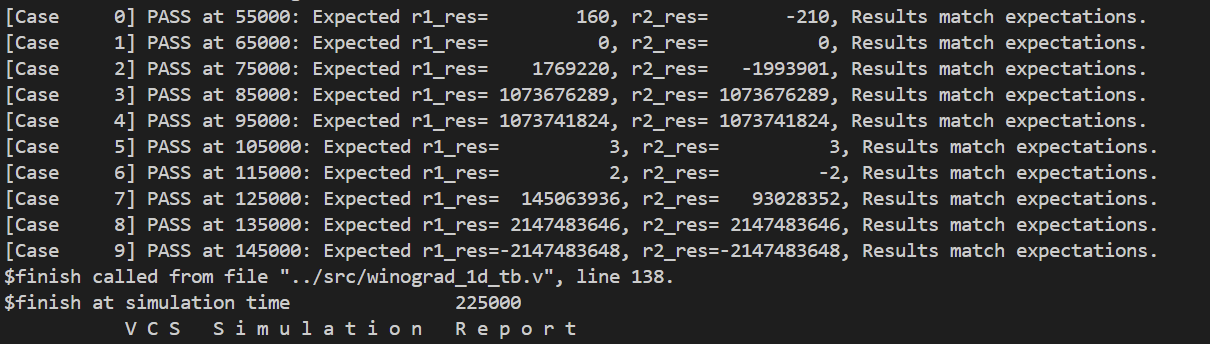
在完成后，你需要运行testbench来验证模块的功能。Testbench中包括计算的Golden Model，会自动比较你编写的模块输出与标准结果。

程序结构

在课程共享文件的 /mnt/course_files 文档下，你能看到 Lab1 文件夹，其中 winograd 文件夹包含了此任务需要的代码。

├── run
│   ├── Makefile
│   └── winograd.f
└── src
    ├── input_transform.v (此处需要填空)
    ├── output_transform.v (此处需要填空)
    ├── weight_transform.v (此处需要填空)
    ├── winograd_1d_tb.v
    └── winograd_1d.v (此处需要填空)

Testbench 运行方法

不显示波形

进入 run 目录，运行 make rerun 即可运行模拟，同时不会显示波形，由于该操作不依赖于GUI，可以在VS Code中直接使用。由于在testbench中设置了 $monitor 命令，会输出不同时刻的计算结果，可以用于验证结果是否正确。

显示波形（使用verdi）

配合Verdi，可以显示电路运行过程中的波形。进入 run 目录，运行 make all 即可进行模拟并显示波形。由于依赖GUI，这一步骤需要使用远程桌面。

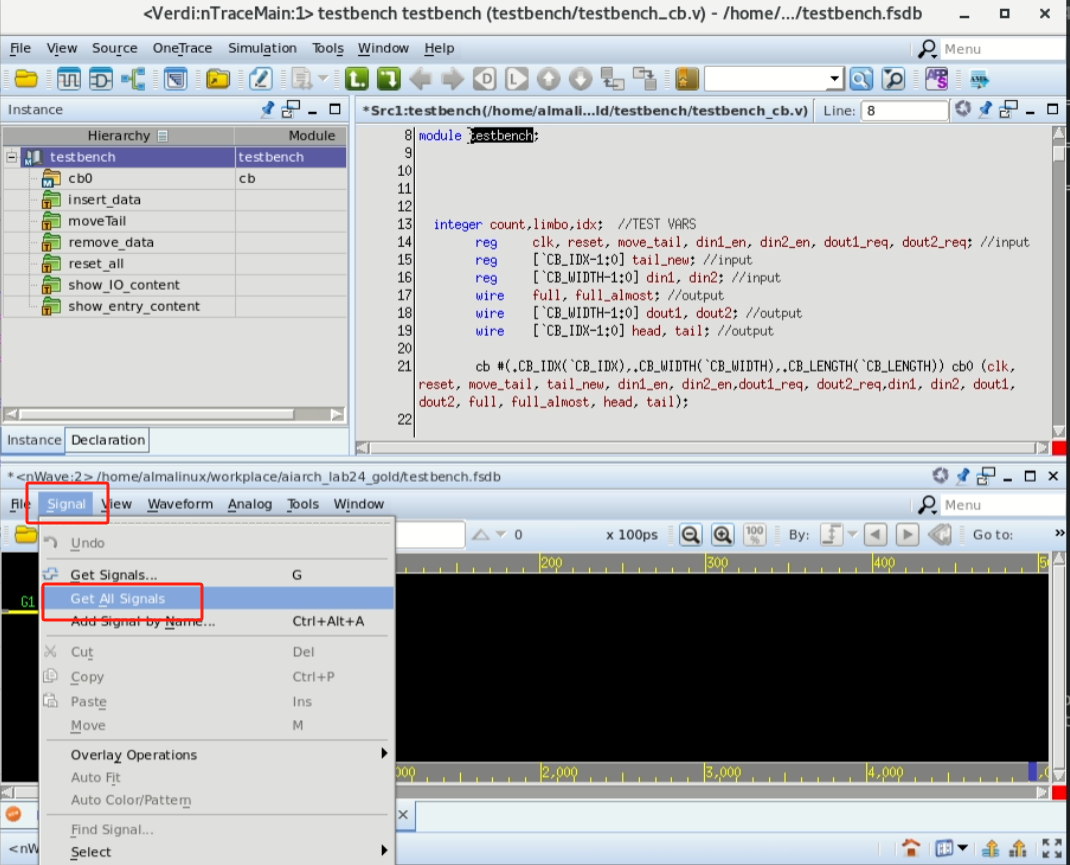
如运行成功，会自动弹出Verdi窗口，在Verdi窗口中，选择下方 Signal - Get All Signals 即可显示所有波形。

清除运行产生的临时文件

只要运行 make clean 即可清除所有运行产生的临时文件。

2. CORDIC算法 (50pts)

背景知识

• CORDIC（COordinate Rotation DIgital Computer）算法是一种基于迭代逼近的方法，通过一系列简单的加减法、移位以及查表操作实现三角函数等的计算。这种算法适用于硬件实现，无乘法器，降低芯片复杂度和功耗，特别适用于 FPGA、ASIC 等嵌入式系统。

• 工作原理：CORDIC 算法通过逐步旋转向量，将目标角度分解为一系列预定义的基本旋转角，每次旋转只需执行移位和加减法操作，从而逼近最终的旋转结果。算法可用于两种模式：旋转模式（计算旋转后的坐标）和向量模式（求取向量的幅值和相位）。

• 关于CORDIC具体的介绍可以参考以下资料：
  • CORDIC算法原理详解

任务介绍

本Lab中，你需要完成一个旋转模式的CORDIC计算模块，代码主体已经提供，你需要完成代码填空。

模块仅包含一个文件 cordic.v ，需要完成计算，你需要完成以下步骤：

1. 由于CORDIC算法的收敛范围有限，你需要在开始迭代前，通过三角恒等变换，将输入转换到合适的象限；

2. 进行迭代计算，本程序中设定的迭代次数为16次。

在完成后，你需要运行testbench来验证模块的功能。Testbench中包括计算的Golden Model，会自动比较你编写的模块输出与标准结果。

程序结构

在课程共享文件的 /mnt/course_files 文档下，你能看到 Lab1 文件夹，其中 cordic 文件夹包含了此任务需要的代码。

├── run
│   ├── cordic.f
│   └── Makefile
└── src
    ├── cordic_tb.sv
    └── cordic.v (此处需要填空)

Testbench 运行方法

Testbench 运行方法与 Winograd的一致。可以参考上方的介绍。

3. Bonus (Extra 50pts)

如有兴趣完成bonus任务，完成其一即可拿到bonus分数。

实现基于CORDIC的FFT

要完成此项任务，你需要完成一个8-point DIT-FFT

FFT 是一种将离散傅里叶变换（DFT）高效计算的算法。

Cooley–Tukey 算法是最常见的 FFT 实现方法，通过递归地将 DFT 分解成若干较小的 DFT，从而大幅降低计算复杂度。利用“蝶形运算”（butterfly operation），将输入数据按照特定方式重新组合，并在递归分解过程中使用周期性和对称性的特性进行高效计算。

可以参考Project页面提供的资料。

2D Winograd

2D Winograd可以由1D Winograd外推得到，假设一个卷积核尺寸为3x3的二维卷积，假设每次我们输出2x2个卷积点，则我们形式化此问题：F(2x2, 3x3)，你需要实现的模块就为这一尺寸。
因为输出为2x2，卷积核大小为3x3，对应的输入点数应该为4x4。

可以表示为：

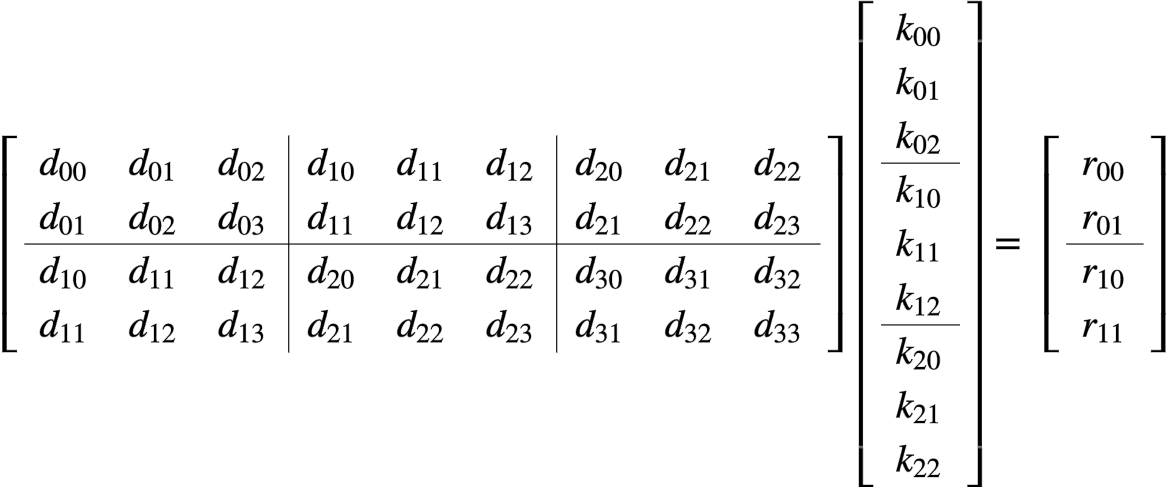
也就是分块矩阵：

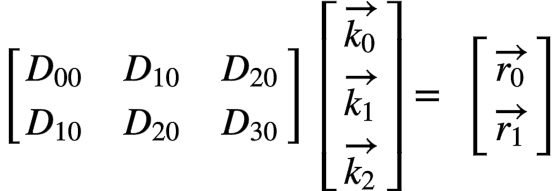
形式上与1D Winograd就一致了。

可以参考Project页面提供的资料。